resumen
Este artículo trata sobre el desarrollo de la creatividad de los estudiantes desde el proceso de enseñanza-aprendizaje y tiene como objetivo proponer una metodología, centrada en enfoque profesional de los contenidos, para el desarrollo de la creatividad de los estudiantes de la Carrera Contabilidad y Finanza desde el proceso de enseñanza-aprendizaje del Cálculo Diferencial e Integral. Su realización estuvo guiada por un enfoque mixto que facilitó el análisis teórico y práctico, desde posiciones cuantitativas y cualitativas que exigieron de la utilización de métodos teóricos, empíricos y estadísticos-matemáticos para profundizar en el tema objeto de estudio. Se utilizó el análisis de documentos, la revisión del producto de la actividad, la observación y la entrevista para recolectar información sobre el nivel de desarrollo de la creatividad de los 12 estudiantes participantes en la investigación; que luego se interpretaron mediante el uso de la estadística descriptiva y se valoraron cualitativamente. Su principal resultado es la metodología, contentiva de procedimientos, orientaciones metodológicas para su implementación y ejemplos que ilustran su empleo en la práctica; su evaluación, mediante el criterio de expertos, ofreció opiniones favorables en cuanto a su calidad y a las posibilidades de aplicación práctica; por lo que se recomienda su contextualización a otros temas de la asignatura y el diseño de nuevas tareas docentes.
PALABRAS CLAVE: Cálculo diferencial e integral, Creatividad, Enfoque profesional, Matemática, Metodología, Proceso de enseñanza-aprendizaje.
ABSTRACT
This article discusses the development of student creativity through the teaching-learning process and aims to propose a methodology focused on a professional approach to content, to foster creativity in students pursuing an Accounting and Finance degree through the teaching-learning process of Differential and Integral Calculus. The research was guided by a mixed approach, facilitating both theoretical and practical analysis from quantitative and qualitative perspectives. This required the use of theoretical, empirical, and statistical-mathematical methods to delve deeper into the subject. Document analysis, product review of the activities, observation, and interviews were used to gather information on the level of creativity development among the 12 students participating in the study. The results were then interpreted using descriptive statistics and qualitatively assessed. The main outcome of this research is a methodology, which includes procedures, methodological guidelines for its implementation, and examples illustrating its practical use. Its evaluation, based on expert feedback, yielded positive opinions regarding its quality and practical applicability. Therefore, its adaptation to other topics within the course and the design of new teaching tasks is recommended.
KEYWORDS: Differential and Integral Calculation, Creativity, Professional Focus, Mathematics, Methodology, Teaching-Learning Process.
INTRODUCción
Las transformaciones que definen el mundo y su acelerado desarrollo exigen la formación de profesionales creativos, capaces de asumir los desafíos de la contemporaneidad. En este sentido, Ríos y Bravo (2017) reconocen como reto de las universidades la formación de profesionales capaces de resolver los problemas sociales, económicos y políticos de las nuevas sociedades.
Al respecto, Saborido (2020) insiste en la pertinencia de estimular aprendizajes autónomos y colaborativos. En consecuencia, la Carrera Contabilidad y Finanzas en Cuba precisa como función profesional la aplicación de procedimientos para la gestión de costos, a través de su planeación, cálculo, análisis y control; y en efecto, la disciplina Matemática exige la aplicación de procedimientos y modelos matemáticos para describir, analizar y evaluar variables económicas y tomar decisiones empresariales adecuadas (Ministerio de Educación Superior de Cuba, 2017).
Por otra parte, al estudiar el proceso de enseñanza-aprendizaje (PEA) de la Matemática, se identifica la necesidad de potenciar el desarrollo de la independencia cognoscitiva y de la creatividad de los estudiantes (Álvarez et al., 2014) y que sus contenidos ofrezcan un campo propicio para desarrollar la creatividad, al encontrar aplicación práctica y vías de solución distintas a una misma problemática (Ballester et al., 2018).
De ahí el rol esencial que tiene el aprendizaje de los contenidos del Cálculo Diferencial e Integral (CDI) en la citada carrera, pues aportan a la comprensión y solución de problemáticas de la profesión. Para Jara (2017) el CDI facilita la solución de problemáticas afines a la determinación del coeficiente de desigualdad en los ingresos, el valor de superávit y la maximización de utilidad, entre otras. Sus ideas denotan la necesidad de desarrollar la creatividad del estudiante al aplicar el CDI; de ahí el interés de los autores en el estudio de esta temática.
Al profundizar en la creatividad y su desarrollo se revisaron los referentes teóricos de autores que la analizaron desde una perspectiva general; destacándose los aportes de De Bono (2000), De Prado (2005), Guilford (1980), Osborn (1953) y Torrance (1979) quienes se enfocaron en el proceso creativo y en el desarrollo del pensamiento. En tanto, en el contexto educativo, Calero (2005), De la Torre (2003) y Díaz y Mitjáns (2013) dieron una concepción holística que pondera la motivación y la influencia del profesor en el desarrollo creativo.
Particular interés tiene el criterio de Concepción et al. (2017) al explicar la creatividad como un proceso concreto que permite elaborar productos nuevos y valiosos y manifestar las relaciones, características y experiencias del sujeto creador en un contexto específico.
Desde la Didáctica de la Matemática, existen estudios que aportan referentes teóricos específicos; entre ellos, Armada et al. (2016) señalan que todo razonamiento matemático incluye una gran dosis de creatividad y reconocen que la creatividad es parte en sí misma de la actividad matemática.
Igualmente, Ayllón et al. (2016) refieren que el pensamiento matemático exige hacer conjeturas y discernir entre las diferentes opciones que permiten resolver una situación dada, lo que a su juicio potencia el desarrollo de la creatividad. Por su parte, Fortes y Andrade (2019) consideran los problemas no rutinarios, con múltiples vías de solución y los problemas abiertos como medio fundamental para el desarrollo de la creatividad.
Por otra parte, para Moreno (2019) el PEA de la Matemática permite la reinvención de lo conocido; condición necesaria para descubrir hechos nuevos y ello requiere de procesos que estimulen el desarrollo de la creatividad como la autonomía, la imaginación y la capacidad de reflexionar, argumentar, elaborar hipótesis y de tomar decisiones. Así mismo, Chávez y Rojas (2021) afirman que la creatividad en matemática considera los logros de la historia educativa de los estudiantes; se caracteriza por la habilidad para producir ideas o soluciones originales a una nueva situación o a problemas aprendidos previamente.
De esta manera, los autores destacan la importancia del desarrollo de la creatividad desde el PEA de la Matemática, reconocen las potencialidades de sus contenidos para ello y revelan los fundamentos teóricos esenciales a considerar. No obstante, no se encontraron propuestas generales y, tampoco específicas que sugieran a los profesores el cómo lograr el desarrollo de la creatividad en los estudiantes durante el PEA del CDI. De ahí que el artículo se enfoque en la temática del desarrollo de la creatividad desde el PEA del CDI.
Es por ello que se requiere responder la siguiente interrogante: ¿qué metodología puede propiciar el desarrollo de la creatividad de los estudiantes de la Carrera Contabilidad y Finanzas, en el PEA del CDI?
El objetivo del artículo es proponer una metodología centrada en el enfoque profesional de los contenidos para propiciar el desarrollo de la creatividad de los estudiantes de la Carrera Contabilidad y Finanzas, en el PEA del CDI. Se organiza en tres apartados: el primero, precisa el marco teórico referencial en que se sustenta la metodología diseñada para el desarrollo de la creatividad de los estudiantes; el segundo, describe la metodología empleada durante el proceso investigativo y, en el tercero, se analizan los resultados del diagnóstico inicial realizado a los participantes; los que permiten diseñar la metodología que se pone a discusión.
Marco teórico referencial en que se sustenta la metodología diseñada para el desarrollo de la creatividad de los estudiantes
En este apartado se precisan las posiciones teóricas que sustentan la metodología desde tres aristas que se interrelacionan: el PEA desarrollador de la Matemática y del CDI, el desarrollo de la creatividad y el enfoque profesional de los contenidos en el contexto de la Carrera Contabilidad y Finanzas.
Primeramente, en la metodología se analiza desde el carácter desarrollador del PEA al promover el desarrollo integral de la personalidad del estudiantado; potenciar su tránsito hacia la independencia y la autorregulación; desarrollar la capacidad de conocer, controlar y transformarse a sí y a su medio creadoramente a la vez que asegura el aprendizaje a lo largo de la vida (Santos y Armas, 2018).
De ahí que se asuma, desde la Didáctica de la Matemática, el criterio de Ballester et al. (2018) en torno a que el proceso de enseñanza-aprendizaje desarrollador es:
Un sistema en el cual tanto la enseñanza como el aprendizaje son subsistemas que garantizan la apropiación activa, creadora, reflexiva, significativa y motivada del contenido como parte de la cultura general integral, teniendo en cuenta el desarrollo actual, con el propósito de ampliar continuamente los límites de la zona de desarrollo próximo potencial. Ello implica una comunicación afectiva y el desarrollo de actividades intencionales, cuyo accionar didáctico genere estrategias de aprendizaje que permitan aprender a aprender Matemática, como expresión del desarrollo constante de una personalidad integral y autodeterminada del estudiante. (p. 13)
Y en correspondencia con la definición, Gibert y Ballester (2013) se retoman tres dimensiones: la activación-regulación, la significatividad y la motivación para aprender. La primera, incluye la actividad intelectual, productiva y creadora; así como la reflexión-regulación metacognitiva. La segunda, se conforma de las relaciones significativas para el aprendizaje y su implicación en la formación de sentimientos actitudes y valores y, la tercera, por motivaciones intrínsecas, autovaloraciones y expectativas positivas hacia el aprendizaje.
También, los lineamientos del enfoque metodológico de la asignatura Matemática (Álvarez et al., 2014) constituyen un referente; estos se expresan en las ideas teóricas que constituyen características del PEA del CDI dado su significado para describir procesos y fenómenos propios de la Contabilidad y Finanzas. Entre ellas destacan: la utilización de la modelación y de los problemas como estrategias de aprendizaje que posibilitan al estudiantado formularse conjeturas, argumentar y validar la aplicación del CDI; la integración efectiva entre el profesor, el estudiante, el conocimiento y la tecnología en el contexto específico de la carrera (Villenas y Rivas, 2019); el diseño de tareas que exijan transferir entre diferentes formas de representación de un concepto y su uso en situaciones de la vida o del quehacer profesional (Uribe et al., 2020) y el uso de los asistentes matemáticos en el PEA del CDI para revelar las relaciones entre los conocimientos y entre estos y sus experiencias práctica y con su mundo afectivo motivacional (Rojas y Rodríguez, 2021) lo que posibilita mayor dinamismo e interactividad.
En segundo lugar, la metodología tiene como referentes los estudios que se relacionan con la creatividad y su desarrollo. Esta se entiende como expresión de la personalidad del sujeto (Mitjáns, 2013) y se analiza que atiende los procesos cognitivos y afectivos, el producto, las características personológicas y las condiciones económicas y sociales (Concepción et al., 2017).
También se considera el vínculo entre matemática y creatividad según los procesos mentales de los estudiantes (Yánez, 2016); que el razonamiento matemático tiene una alta dosis de creatividad, pues implica el surgimiento de nuevas ideas, el descubrimiento de una o varias soluciones y la identificación o formulación de nuevos problemas (Armada et al., 2016); que el pensamiento matemático exige conjeturar y discernir entre las diferentes vías de solución de la tarea (Ayllón et al., 2016) y la variada aplicación práctica de los conocimientos matemáticos. Al respecto, se asumen, los criterios de Ballester et al. (2018) sobre la creatividad en el PEA de la Matemática, al verla como:
Un tipo de actividad humana compleja, encaminada a la obtención o reproducción de nuevos valores materiales o espirituales. Ella se manifiesta en la disposición y capacidad de los alumnos; para trabajar independiente e individualmente, en su originalidad y racionalidad para el análisis de situaciones y soluciones a problemas, y en su capacidad para transferir los conocimientos, hechos y fenómenos conocidos a situaciones nuevas. (p. 26)
Al respecto, los autores del artículo insisten en las potencialidades que ofrece la resolución de problemas para el desarrollo de la creatividad y viceversa; pero acotan que el estudiante puede ser creativo o desarrollar su creatividad durante la solución de cualquier tipo de tarea matemática, ya que la creatividad se entiende desde una perspectiva teórica que articula los procesos cognitivos y afectivos, las características personológicas y las condiciones sociales.
Sobre el desarrollo de la creatividad, expresa la unidad entre lo cognitivo y lo afectivo (Concepción et al., 2017), constituye un desafío para la educación superior al tener que formar egresados aptos para la producción e innovación en su contexto (Zambrano, 2019), se logra si sistemáticamente se establecen relaciones entre los conocimientos, la investigación y la imaginación (De La Fuente et al., 2019) y exige una actitud constructiva y de confianza en las potencialidades de los estudiantes (Quimis et al., 2019).
De igual modo, el PEA de la Matemática permite reinventar lo conocido y descubrir hechos matemáticos nuevos; a juicio de Sánchez et al. (2022) plantea que existen recursos en la Didáctica de la Matemática que promueven el desarrollo de la creatividad: los procedimientos heurísticos, los asistentes matemáticos y la resolución de problemas; vistos como estrategias creativas.
Constituyen como fundamentos de la metodología los estudios que, si bien se enfocan en otros contenidos matemáticos y niveles educativos, tienen como fin el desarrollo de la creatividad. Al respecto, se precisa el valor de preparar a los estudiantes para predecir resultados e investigar sobre el nuevo conocimiento en función de robustecer el ingenio (De La Fuente et al., 2019) y de estimular el pensamiento divergente a partir de la resolución de problemas (Chávez y Rojas, 2021).
Por otra parte, se asume la utilización de recursos heurísticos como estrategia que enseña a pensar y crear; así como las funciones cognoscitivas de una tarea creativa en el PEA de la Matemática: detectar y formular nuevos problemas, encontrar nuevos conocimientos y vías novedosas y originales para solucio¬narlas; así como proponer nuevas vías de solución y soluciones a problemas ya resueltos (Armada et al., 2016).
Y, en tercer lugar, la metodología se basa en el enfoque profesional del PEA, pues este tiene la finalidad de orientar y motivar al estudiante hacia la profesión en que se forma (Lao et al., 2020) a partir del CDI; reconoce como una tarea de los profesores universitarios la contextualización del aprendizaje al perfil de la profesión (Minaya, 2017), exige la utilización de tareas relacionadas con el perfil profesional de la carrera que estimulen la motivación y el valor de los problemas de la profesión que se resuelven con la aplicación integrada de los contenidos disciplinares (Rodríguez, 2018).
En consonancia, los contenidos del CDI se deben abordar desde una perspectiva profesional que se relacione con el perfil de cada carrera (Rojas y Rodríguez, 2021) y su PEA debe enfocarse hacia el trabajo con los problemas propios de la profesión y en función del desarrollo de las habilidades profesionales a las que permiten dar solución (Valdés y Páez, 2021).
En particular, se reconocen las posibilidades de la matemática para modelar situaciones reales o simuladas de una profesión (Ramírez, 2016); la variedad de los problemas profesionales de la contabilidad y las finanzas que se modelan o resuelven aplicando el CDI (Viñamagua, 2017) y que estos conocimientos se relacionan con la optimización de funciones de ingreso, costo y beneficio (Minaya, 2017); así como la determinación del costo aproximado de producir o vender un producto a partir del análisis marginal (Villena y Rivas, 2019).
Metodología
Este apartado describe el camino metodológico que se utilizó en la investigación que da origen al artículo; el mismo siguió un enfoque mixto que integra lo cuantitativo y lo cualitativo en función de una mejor comprensión teórica y práctica del tema objeto de estudio, lo que implicó la recolección y el análisis de datos.
Este enfoque exigió utilizar métodos teóricos y empíricos que permitieron ahondar en la naturaleza compleja del desarrollo de la creatividad. De los teóricos, el histórico-lógico facilitó determinación del estado del arte y la precisión del marco teórico referencial; el sistémico, hizo posible establecer relaciones entre las características del PEA del CDI y las vías para desarrollar la creatividad y el inductivo-deductivo, facilitó la realización de inferencias relacionadas con el nivel de desarrollo de la creatividad en el referido proceso.
De los métodos empíricos se utilizó el análisis de documentos, para estudiar las exigencias y orientaciones metodológicas del PEA del CDI y sus potencialidades para el desarrollo de la creatividad; la revisión del producto de la actividad y la observación, aportaron información sobre el nivel de desarrollo de la creatividad de los estudiantes en diferentes momentos de la investigación. La entrevista, la revisión del producto de la actividad y la observación aportaron información asociada al desarrollo de la creatividad desde las experiencias de los estudiantes y profesores participantes. En cada caso se diseñó una guía con los aspectos de interés a tener en cuenta.
Para la validación de los instrumentos, previo a su utilización, se aplicaron a otros sujetos con características similares y se sometieron al análisis, mediante una sesión en profundidad, por parte de especialistas en estudios sobre el desarrollo de la creatividad; lo que condujo a su perfeccionamiento y diseño definitivo.
En consecuencia, se consideró como unidad de estudio a los estudiantes de la Carrera Contabilidad y Finanzas de la Universidad de Sancti Spíritus José Martí Pérez. Se seleccionó una muestra no probabilística e intencional conformada por los doce (12) estudiantes del primer año que representan el 100 % de la matrícula y el 21,8 % del total de la matrícula de la carrera. El motivo de la selección respondió a que es en este año donde se imparten los contenidos del CDI.
Los estudiantes tenían como características comunes el haber logrado resultados similares en el examen de ingreso a la universidad y en los temas previos a la introducción del CDI, la mayoría de ellos creía complejo el estudio del CDI y no comprendía el vínculo de este contendido con la profesión. De igual modo, les interesaba aprobar la asignatura y manifestaban tendencia a crear sus propias estrategias de aprendizaje.
Resultados y discusión
En este apartado se analizan los resultados del diagnóstico inicial realizado a los participantes en la investigación, del cual emergieron potencialidades y dificultades que se tuvieron en cuenta al diseñar la metodología que se pone a discusión.
Para el diagnóstico se analizó la variable de estudio: nivel de desarrollo de la creatividad de los estudiantes de la Carrera Contabilidad y Finanzas en el PEA del CDI; la que se expresa mediante los rasgos personológicos asociados al proceso creativo: motivación, originalidad e independencia cognoscitiva; en unidad con las posibilidades de los estudiantes para transitar por sus fases según el contenido. Al respecto, se identificaron las dimensiones e indicadores siguientes.
La motivación (D1) expresa la: necesidad (I.1.1), disposición (I.1.2) y satisfacción (I.1.3) de los estudiantes por la solución de las tareas del PEA del CDI. La originalidad (D.2) expresa la: producción de ideas novedosas (I.2.1), racionalidad (I.2.2) y transferencia de conocimientos y habilidades matemáticas (I.2.3) de los estudiantes durante la solución de las tareas.
La independencia cognoscitiva (D.3) expresa las: posibilidades de los estudiantes para utilizar diferentes fuentes de información (I.3.1), orientarse ante situaciones matemáticas y profesionales diversas (I.3.2) y defender sus criterios en relación a las vías de solución y a los resultados obtenidos (I.3.3).
La información que se describe se deriva de los datos que emanaron de la aplicación de los métodos que se relacionan; para ello se consideró como unidad de análisis la tarea docente que exige del CDI para su solución.
Se obtuvieron datos al observar al aplicar cada instrumento, en las guías elaboradas se incluyeron los indicadores descritos en forma de preguntas o aspectos a valorar. Su análisis se enriqueció con el estudio caso a caso del desempeño de cada estudiante.
Al triangular los datos obtenidos luego de la aplicación de los métodos descritos se analizó el comportamiento de los indicadores y su influencia en las dimensiones y en la variable de estudio. Para su medición se utilizó una escala nominal de cinco categorías: muy adecuada (MA), bastante adecuada (BA), adecuada (A), poco adecuada (PA) e inadecuada (I).
Los indicadores se evaluaron de forma directa a partir de la escala precisada y las dimensiones a partir del índice promedio de sus indicadores. Primero, se le asoció a la evaluación de cada indicador un valor de la lista (100, 75, 50, 25 y 0); luego, al promedio resultante se le hizo corresponder con uno de los intervalos de valores siguientes: [0, 20), [20, 40), [40, 60), [60, 80) y [80, 100] y, finalmente, se le asoció el valor de la escala según el intervalo (MA, BA, A, PA y I) que le correspondía. Para evaluar la variable se aplicó el proceder antes descrito.
La Tabla 1 muestra el resultado la evaluación de los indicadores y, a partir de ellos, se evaluaron las dimensiones y la variable de estudio.
Tabla 1.
Resultados de la evaluación final de los indicadores
|
Est.
|
Dimensión 1
|
Dimensión 2
|
Dimensión 3
|
|
1.1
|
1.2
|
1.3
|
1.1
|
1.2
|
1.3
|
2.1
|
2.2
|
2.3
|
2.1
|
2.2
|
2.3
|
3.1
|
3.2
|
3.3
|
3.1
|
3.2
|
3.3
|
|
1
|
A
|
PA
|
PA
|
50
|
25
|
25
|
PA
|
PA
|
I
|
25
|
25
|
0
|
I
|
I
|
I
|
0
|
0
|
0
|
|
2
|
BA
|
PA
|
PA
|
75
|
25
|
25
|
PA
|
PA
|
I
|
25
|
25
|
0
|
I
|
I
|
I
|
0
|
0
|
0
|
|
3
|
PA
|
PA
|
PA
|
25
|
25
|
25
|
I
|
I
|
I
|
0
|
0
|
0
|
PA
|
I
|
I
|
25
|
0
|
0
|
|
4
|
PA
|
PA
|
I
|
25
|
25
|
0
|
I
|
I
|
I
|
0
|
0
|
0
|
I
|
I
|
I
|
0
|
0
|
0
|
|
5
|
BA
|
A
|
PA
|
75
|
50
|
25
|
A
|
PA
|
PA
|
50
|
25
|
25
|
A
|
PA
|
I
|
50
|
25
|
0
|
|
6
|
BA
|
BA
|
BA
|
75
|
75
|
75
|
BA
|
A
|
A
|
75
|
50
|
50
|
A
|
I
|
PA
|
50
|
0
|
25
|
|
7
|
A
|
PA
|
BA
|
50
|
25
|
75
|
PA
|
A
|
PA
|
25
|
50
|
25
|
I
|
PA
|
I
|
0
|
25
|
0
|
|
8
|
PA
|
I
|
PA
|
25
|
0
|
25
|
I
|
I
|
I
|
0
|
0
|
0
|
I
|
I
|
I
|
0
|
0
|
0
|
|
9
|
A
|
PA
|
PA
|
50
|
25
|
25
|
PA
|
I
|
I
|
25
|
0
|
0
|
I
|
I
|
I
|
0
|
0
|
0
|
|
10
|
A
|
I
|
I
|
50
|
0
|
0
|
PA
|
PA
|
PA
|
25
|
25
|
25
|
PA
|
PA
|
I
|
25
|
25
|
0
|
|
11
|
A
|
PA
|
I
|
50
|
25
|
0
|
PA
|
I
|
I
|
25
|
0
|
0
|
I
|
I
|
I
|
0
|
0
|
0
|
|
12
|
PA
|
PA
|
PA
|
25
|
25
|
25
|
I
|
I
|
I
|
0
|
0
|
0
|
I
|
I
|
I
|
0
|
0
|
0
|
Fuente: Elaboración propia.
La Figura 1 muestra el promedio de la evaluación final de cada dimensión y de la variable. Este se obtuvo al promediar el valor obtenido por cada estudiante en los indicadores correspondientes a cada dimensión y, luego, para la variable se calculó el promedio del resultado de las tres dimensiones.
Se confirma un comportamiento poco favorable en las tres dimensiones y en la variable, al observarse que el promedio en ningún caso supera los 35 puntos de un valor máximo de 100. La dimensión con mejor resultado fue la motivación por la realización de las tareas docentes de CDI, que obtiene un valor promedio de 34. La originalidad muestra un valor promedio de 16,7 y la independencia cognoscitiva alcanza un promedio de 6,9; se constata así que ambas dimensiones obtuvieron evaluación de I; mientras que la motivación alcanzó la categoría PA. De este modo, la variable obtuvo un valor promedio de 19,2 que resulta en la categoría I, lo que demuestra el limitado desarrollo de la creatividad de los estudiantes.
Figura 1.
Promedio de la evaluación de las dimensiones y de la variable de estudio
Fuente: Elaboración propia.
Estos resultados se enriquecieron con las valoraciones cualitativas que expresan potencialidades y dificultades a partir del estudio individualizado del desempeño de los estudiantes. Entre las primeras, se valoró que los estudiantes:
● Comprenden la necesidad de aprender a derivar e integrar para poder aprobar la asignatura Matemática y otras propias de la carrera.
● Analizan las exigencias de las tareas e identifican lo dado y lo buscado; cuando se trata de propiedades y reglas de derivación e integración.
● Seleccionan ideas de otros para lograr la solución de las tareas matemáticas de cálculo de derivadas o integrales menos complejas.
● Prefieren utilizar fuentes de información que se sustentan en las TIC y exponen el resultado obtenido al realizar las tareas.
Entre las dificultades más comunes se destacó que los estudiantes:
● Se muestran inseguros y dependientes al solucionar las tareas de cálculo de derivadas o integrales complejas vinculadas a los problemas profesionales.
● Resultan poco curiosos al tener que problematizar en torno las tareas de CDI que exigen una interpretación desde lo profesional.
● No logran modelar situaciones profesionales aplicando los conocimientos y habilidades matemáticas propias del CDI.
● Generan ideas poco novedosas y enfocadas en una única vía de solución de las tareas; las que no resultan en materiales que faciliten su aprendizaje.
● No comprenden las situaciones profesionales que le son presentadas utilizando objetos matemáticos correspondientes al tema de CDI.
Los resultados reafirmaron como una de las causas que incide en el desarrollo de la creatividad de los estudiantes de la Carrera Contabilidad y Finanzas en el PEA del CDI el limitado vínculo entre los contenidos y la profesión; hecho que se justifica también en las siguientes notas de campo tomadas durante la observación del desempeño de los estudiantes: “para qué me sirve esto en mi carrera” (sujeto 1, noviembre de 2022) , “no entiendo el significado práctico del resultado” (sujeto 4, noviembre de 2022) y “en las entidades y empresas que visitamos no vemos la utilización de este contenido” (sujeto 7, noviembre de 2022) entre otras. De ahí, el diseño de una metodología que centre su accionar en el enfoque profesional de los contenidos que se relacionan con el CDI.
Para los autores del artículo, la metodología precisa de exigencias que orienten la manera de actuar, a partir de métodos y procedimientos que faciliten el cumplimiento de un objetivo (Leyva, 2013). Además, si es una metodología para el PEA, entonces orienta al profesor y a los estudiantes hacia el uso de métodos, medios y procedimientos que permitan el logro de los objetivos.
En este caso, su presentación se estructura en: objetivo general, fundamentación, aparato teórico e instrumental, recomendaciones para su instrumentación, formas de evaluación y su representación gráfica (Alonso et al., 2019). De manera particular, la metodología en su aparato instrumental describe los procedimientos que, apoyados en la estructura externa de los métodos que aseguran el uso del enfoque profesional del contenido y el desarrollo de la creatividad, indican las acciones a realizar por parte de los profesores y estudiantes en el PEA del CDI.
Seguidamente se presenta la metodología que se diseñó como respuesta a la interrogante que guío el proceso investigativo. Su objetivo general es: desarrollar, a partir del enfoque profesional, la creatividad de los estudiantes de la Carrera Contabilidad y Finanzas en el PEA del CDI.
Se consideran como fundamentos las posiciones teóricas asumidas con relación al PEA del CDI, las relativas al desarrollo de la creatividad y al enfoque profesional; visto como su rasgo distintivo y como vía para desarrollar la creatividad; es por ello que se utilizan situaciones vinculadas a la profesión y que pueden resolverse aplicando el CDI.
La metodología, considera como contexto general el proceso de formación profesional de la Carrera Contabilidad y Finanzas y, particular, el PEA del CDI en la propia carrera. Su alcance está determinado por la capacidad de los profesores para utilizar los procedimientos que esta precisa para asegurar el desarrollo de la creatividad de los estudiantes desde el enfoque profesional del PEA del CDI.
El aparato teórico-cognitivo, considera en su cuerpo categorial: definiciones, categorías y exigencias. Entre las definiciones que considera están: el PEA desarrollador, creatividad, desarrollo de la creatividad y enfoque profesional.
Dado el rol que asumen en el aparato instrumental, se analizan las definiciones de: problema profesional, tarea docente, estrategia creativa e integración. La tarea docente se asume como “aquella actividad que se concibe para realizar por el alumno en la clase y fuera de esta, vinculada a la búsqueda y adquisición de los conocimientos y al desarrollo de habilidades” (Rico y Silvestre, 2002, p. 78).
La integración se asume como:
La concatenación de los conocimientos, habilidades y valores a desarrollar que reflejan los vínculos internos entre las diferentes disciplinas y contribuyen al logro de un modo de actuación en los alumnos para aplicar lo aprendido, interpretar e interactuar con el contexto cultural al que pertenecen (Vázquez, 2003).
Además, se tiene en cuenta que el vínculo universidad-sociedad se concreta una realidad histórica, una concepción de la profesión y su rol social (Ministerio de Educación Superior de Cuba, 2016) y determina las acciones a realizar desde el proceso formativo para lograr modos de actuación profesional en el estudiante y acercarlo a su futura profesión.
En su cuerpo legal, la metodología considera el Plan de Estudio como documento que precisa los problemas profesionales y reconoce entre las funciones principales del profesional de la contabilidad y las finanzas la de “proponer con independencia y creatividad posibles soluciones a los distintos problemas de la profesión en búsqueda de la eficiencia y eficacia económica” (Ministerio de Educación Superior de Cuba, 2018, p. 5). Además, atiende, que el programa de la disciplina Métodos Económico-Matemáticos exige “estimular el desarrollo de soluciones creativas a los problemas que el futuro egresado deberá resolver en su práctica profesional” (Ministerio de Educación Superior de Cuba, 2017, p. 2) en integración con otras disciplinas propias de la profesión y con la práctica laboral.
El aparato instrumental, determina cinco procedimientos generales que orientan la actuación del profesor y de los estudiantes en función del desarrollo de la creatividad a partir del enfoque profesional del CDI. Estos procedimientos precisan las acciones que realizaría el profesor en cada momento del PEA del CDI y de los estudiantes durante la ejecución del mismo.
El primer procedimiento, se realiza desde la planificación a mediano y corto plazo del PEA, orienta al profesor hacia la determinación de vínculos entre el CDI y los problemas profesionales. Este precisa las siguientes acciones:
● Identificación de los problemas profesionales con los que se vincula el CDI.
● Determinación de las relaciones intra e interdisciplinarias que sustentan el tratamiento de los problemas profesionales desde el contenido.
● Precisión de los componentes del proceso de formación en que se analiza cada problema profesional según las potencialidades del contenido.
● Selección de posibles métodos, medios y estrategias creativas para el tratamiento de los problemas profesionales a través del contenido.
El segundo procedimiento, se realiza desde la planificación, y orienta al profesor hacia el diseño de las tareas que propician el desarrollo de la creatividad desde el enfoque profesional del CDI. El mismo exige realizar las siguientes acciones:
● Selección del tipo de tarea a diseñar, según las potencialidades del CDI y su vínculo con el problema profesional.
● Determinación de la intención didáctica de la tarea, según el problema profesional y el componente del proceso de formación en que se utilizará.
● Diseño de la tarea a partir de las relaciones entre los componentes del PEA con enfoque profesional.
El tercer procedimiento, direcciona la actuación del profesor durante la ejecución del PEA con enfoque profesional y, en particular, durante la orientación de las tareas. Para ello se recomiendan las siguientes acciones:
● Orientación de la tarea de modo que revele los conocimientos y habilidades matemáticas y el problema profesional con que esta se relaciona.
● Análisis del objetivo de la tarea, de las posibles acciones a realizar y de su aporte a la formación profesional de conjunto con los estudiantes.
● Precisión de los posibles métodos, medios y estrategias creativas a utilizar durante la solución de las tareas.
● Precisión de las formas de control a utilizar para comprobar la solución de la tarea y su impacto en la formación profesional.
El cuarto procedimiento guía la actuación del estudiante durante la solución de las tareas, facilitando su tránsito por las etapas del proceso creativo y su motivación, originalidad e independencia cognoscitiva. Este, incluye las siguientes acciones:
● Problematización en torno al problema profesional que presenta la tarea y su vínculo con el CDI.
● Cuestionamiento de lo conocido y lo desconocido para plantearse hipótesis de trabajo o variadas vías de solución a la tarea según el problema profesional.
● Selección o elaboración de medios y estrategias creativas a utilizar para la solución de la tarea.
● Análisis de las posibles vías de solución de la tarea y de los aprendizajes profesionales que esta implica.
● Exposición e intercambio de las vías utilizadas para la solución de la tarea, de sus resultados y de los productos derivados de su aprendizaje.
A continuación, se ofrecen recomendaciones para la instrumentación práctica de los procedimientos; pues es a través de ellos que se concreta la aplicación de la metodología en la práctica. En todos los casos se ilustran situaciones propias de la profesión del contador que tienen solución aplicando los conocimientos y habilidades propias del CDI y se insiste en el análisis del significado del resultado matemático; atendiendo a la característica que distingue la metodología.
En el caso del primero, se sugiere al profesor el análisis (desde los niveles de trabajo metodológico) del Plan de Estudio y de otros documentos (programas de disciplina, libros de texto, guías de estudio) que le faciliten la identificación de los problemas profesionales a resolver desde el PEA del CDI; el intercambio con profesores de otras disciplinas o profesionales de las unidades docentes para la determinación de los vínculos entre el contenido y la profesión; la determinación de las relaciones entre el contenido y los problemas profesionales a partir de los conocimientos, habilidades y formas de trabajo y de pensamiento propias del CDI y de la profesión; prever los componentes del proceso de formación donde se pueden analizar cada problema profesional y los escenarios que aportarían información de interés para su solución; la elección de métodos problémicos que inciten el trabajo independiente y el uso de medios tradicionales y de las TIC; así como las estrategias y técnicas creativas para que los estudiantes transiten por las fases del proceso creativo.
La Tabla 2 muestra el trabajo con el primer procedimiento, donde se identifican las potencialidades del CDI para la solución de problemas propios de la profesión.
Tabla 2.
Ejemplo de la utilización del procedimiento 1
|
Problema profesional
|
Determinar la validez de la información contable y financiera para la toma de decisiones oportunas.
|
|
Subproblema profesional
|
Maximizar la utilidad de una inversión a partir del análisis de la función que representa (Costo, Ingreso).
|
|
Contenido matemático
|
Aplicación de la derivada (determinar máximo y mínimo y resolver problemas de optimización).
|
|
Relaciones intradisciplinarias
|
Investigación de operaciones (contribuye a la preparación de los estudiantes para optimizar procesos contables y financieros).
|
|
Contenidos de la profesión
|
Análisis de la función utilidad para determinar la rentabilidad de un proceso económico
|
|
Relaciones interdisciplinarias
|
Contabilidad General y Costos
|
|
Componentes y escenarios profesionales
|
Académico y laboral
Organizaciones económicas del estado y formas no estatales de gestión
|
|
Métodos
|
Problémicos (búsqueda parcial heurística)
|
|
Medios
|
Informes sobre la rentabilidad económica (datos) y una hoja de trabajo Excel
|
|
Estrategias creativas
|
Problemas, Modelación, Procedimientos Heurísticos y Usar las TIC
|
Fuente: Elaboración propia.
Para el trabajo con el segundo procedimiento se sugiere la selección del tipo de tarea, según el vínculo entre la actividad matemática y profesional a realizar y el componente del proceso de formación en que esta se usaría (académico, laboral o investigativo); el análisis del conocimiento y de la habilidad matemática que predomina en ella y, también, de la tarea o habilidad profesional con que se relaciona; la determinación de su intención didáctica y, finalmente, su diseño.
Se recomienda que las tareas estimulen la imaginación, el pensamiento y el razonamiento de los estudiantes; ofrezcan la posibilidad de establecer relaciones, de producir nuevas ideas, de transferir conocimientos y de argumentar sus puntos de vista. Se deben considerar como posibles tipos de tareas a utilizar aquellas donde los estudiantes tengan que: determinar Costo, Ingreso y Beneficio Marginal (calcular derivadas), optimizar funciones de Costo, Ingreso y Beneficio (aplicaciones de la derivada), formular problemas relacionados con la profesión (con solución a partir de las aplicaciones de la derivada), determinar el valor del Costo, el Ingreso y el Beneficio a partir de funciones marginales (integración de funciones), determinar el excedente (superávit) de consumidores y de productores (aplicaciones de la integral definida), calcular el total del rubro cuentas por cobrar que superan en determinado tiempos el nivel de equilibrio y analizar la tendencia de las cuentas por cobrar (integrales definidas).
La Tabla 3 muestra el trabajo con el procedimiento que se utiliza para determinar el tipo de tarea que permite vincular el CDI al contenido propio de la profesión.
Tabla 3.
Ejemplo de la utilización del procedimiento 2
|
Problema profesional
|
Determinar la validez de la información contable y financiera para la toma de decisiones.
|
|
Conocimientos matemáticos
|
Cálculo de integrales definidas (áreas entre curvas)
|
|
Habilidades matemáticas
|
Resolver problemas de cálculo de áreas entre curvas.
|
|
Habilidades o tareas profesionales
|
Tomar decisiones económicas en torno al excedente de productores y consumidores.
|
|
Tipo de tarea a diseñar
|
Tareas para la determinación del excedente (superávit) de consumidores y de productores.
|
|
Intención didáctica y componente del proceso de formación
|
Motivación y Académico
|
|
Escenarios profesionales
|
Las organizaciones económicas del estado y las formas no estatales de gestión
|
|
Métodos
|
Problémicos (búsqueda parcial heurística)
|
|
Medios
|
Informes de precio y venta (datos) de organizaciones económicas y de formas no estatales de gestión, hoja de trabajo (opcional)
|
|
Estrategias creativas
|
Problemas, Modelación, Procedimientos Heurísticos y Usa las TIC.
|
Fuente: Elaboración propia.
Seguidamente, aparece una tarea diseñada para la optimización, cuya solución requiere de la determinación de la función Ingreso y del cálculo de su valor máximo a partir del cálculo de la primera derivada.
Una empresa de servicios a domicilio tiene actualmente 550 clientes que pagan una cuota mensual de $ 100.00; si una encuesta reveló que podían tener 160 clientes más por cada $ 10.00 de disminución en la cuota. ¿Bajo qué cuota se obtendrá el ingreso máximo y cuántos suscriptores se tendría entonces?
a) ¿Qué significado tienen estos resultados para la contabilidad de la empresa?
b) ¿Es factible para la empresa el resultado de la encuesta?
c) Elabora, según las vías de solución empleadas, un material o medio donde le sugieras a los directivos de una empresa, cómo resolver esta situación.
Para el trabajo con el tercer procedimiento se sugiere la orientación de la tarea según el diagnóstico de los estudiantes, dejando preciso el momento en que la realizarían y la forma en que se controlará; el análisis, en un ambiente ameno y flexible, de los contenidos matemáticos y del problema profesional a resolver; la precisión y construcción colectiva del objetivo de la misma, lo que requiere plantear y analizar de conjunto con los estudiantes las posibles acciones a realizar y la necesidad de su solución; el intercambio con y entre ellos en relación a los posibles métodos, medios y estrategias creativas a utilizar para la solución de la tarea sin imponer criterios y, para su control, se recomienda ponerlos ante situaciones que le exijan demostrar dominio del contenido y del problema profesional, siempre propiciando el intercambio de diferentes vías de solución y el análisis de los productos elaborados.
La Tabla 4 muestra un modo de orientar una tarea en función del desarrollo de la creatividad de los estudiantes. En este caso la situación que se presenta tiene solución aplicando el cálculo de integrales de integrales definidas.
Tabla 4.
Ejemplo de la utilización del procedimiento 3
|
Tipo de tarea a orientar
|
Orientación de la tarea
|
|
Determinar el valor del ingreso a partir del ingreso marginal (integración de funciones).
Un pozo petrolero que produce 200 barriles de petróleo crudo al día, se agotará dentro de 10 años y ha sido estudiado que dentro de t-meses el precio del petróleo será 30+ 0,5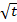 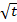 pesos por barril. Suponiendo que el petróleo acumulado en la producción mensual lo vende totalmente al precio de mercado en ese momento, calcular cuál será el ingreso total futuro obtenido en la venta del petróleo extraído del pozo. (ajustado a partir de Moncada, 2002). pesos por barril. Suponiendo que el petróleo acumulado en la producción mensual lo vende totalmente al precio de mercado en ese momento, calcular cuál será el ingreso total futuro obtenido en la venta del petróleo extraído del pozo. (ajustado a partir de Moncada, 2002).
|
Analicemos el siguiente problema para comprender la necesidad profesional de las aplicaciones del cálculo de integrales definidas.
Leamos el problema, y vamos a analizar las siguientes interrogantes: ¿cuáles son los conocimientos y las habilidades matemáticas y profesionales que refleja esta situación? ¿Cómo se puede modelar algebraicamente la función Ingreso a partir de los datos conocidos?
Entonces, el objetivo de la tarea es determinar el ingreso para los 10 años de explotación del pozo utilizando el cálculo de integrales definidas. Para su cumplimiento, que objetivos individuales ustedes se propondrían y que hipótesis de trabajo se estarían formulando a partir de la información del problema.
¿En qué otras situaciones profesionales se puede determinar el ingreso neto de un producto determinado (agotable) a futuro?
A partir del procedimiento seguido para la solución del problema, elabora una herramienta que pueda orientar a futuros inversores sobre la posible rentabilidad de una inversión en este tipo de empresas.
|
Fuente: Elaboración propia.
Para el trabajo con el cuarto procedimiento, por parte de los estudiantes, se le recomienda que problematicen en torno al problema profesional que presenta la tarea y su relación con el CDI; que identifiquen el elemento que provoca la dificultad intelectual (revelar la contradicción) y definan o formulen nuevos problemas que impliquen el uso del CDI; la utilización de los procedimientos heurísticos para cuestionar lo conocido y buscar relaciones con lo desconocido, plantearse posibles hipótesis o vías de solución, poner en duda lo dado y encontrar nuevos conocimientos (conceptos, leyes, relaciones, reglas); la determinación de vías novedosas y originales para llegar al resultado a partir de sus propias elaboraciones utilizando medios y estrategias creativas que le faciliten la exploración y la investigación y que expongan las vías utilizadas para la solución de la tarea creativa, sus resultados y los productos derivados de su aprendizaje.
Seguidamente, se ejemplifica la manera en que los estudiantes pueden asumir el proceso de solución de una tarea a partir de la utilización del programa heurístico general (ver Tabla 5). La situación, vinculada a la tarea profesional se relaciona con la determinación del Ingreso y Beneficio Marginal y se resuelve aplicando el cálculo de derivadas.
Tabla 5.
Ejemplo de la utilización del procedimiento 4
|
Tipo de tarea
|
Determinación del Ingreso y Beneficio Marginal (calcular derivadas)
Un empresario estima que el costo total para producir q unidades por día de un producto p está definido por la ecuación: 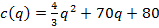 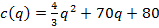 y el precio de venta p por cada unidad es: y el precio de venta p por cada unidad es: 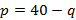 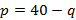 con el fin de realizar un análisis completo de sus operaciones en función de las cantidades a producir y el costo de producir 40 unidades adicionales. con el fin de realizar un análisis completo de sus operaciones en función de las cantidades a producir y el costo de producir 40 unidades adicionales.
|
|
Etapas del programa heurístico general
|
Pasos para la solución de la tarea
|
|
Orientación hacia el problema
|
¿Qué información encuentro en el texto del problema?
El costo y precio del producto.
El precio depende de la cantidad.
¿Qué función depende del precio y la cantidad?
La función ingreso
|
|
Trabajo en el problema
|
¿Qué implica hacer un análisis completo de las operaciones productivas? Determinar los ingresos, costos y beneficios totales y marginales.
¿Qué funciones necesito para hacer el análisis completo de las operaciones productivas en este caso? La función ingreso, costo y beneficio. La función costo ya la tengo.
¿Cómo determino cada función?
Función ingreso: establezco relación precio – cantidad.
Función beneficio: establezco relación ingreso - costo
|
|
Solución del problema
|
La relación precio – cantidad es:
I(q) = p.q = (40 – q)q = 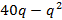 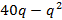
Entonces, derivo I(q) para determinar el ingreso marginal: I´(q) = 40 – 2q
La relación ingreso – costo es: B (q) = I (q) – c (q)
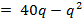 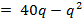 - -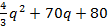 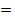 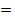 - -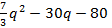 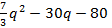
Entonces, derivo B (q) para determinar el beneficio marginal: 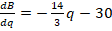 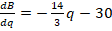
¿Qué significa hallar el costo de producir 40 unidades adicionales? Derivar la función costo y evaluar en una cantidad. c´(q) =   q + 70, c´(40) = = q + 70, c´(40) = =   (40) + 70 = 176.67 (40) + 70 = 176.67
|
|
Evaluación de la vía de solución
|
¿Qué inferencias y decisiones profesionales puedo derivar del resultado obtenido?
Intercambio con los demás estudiantes para ver si utilizaron otras vías de solución
Elaboro un material que describa el procedimiento a seguir en este tipo de situación profesional.
Sugiero buscar en los escenarios profesionales situaciones semejantes a esta y resolverlas.
|
Fuente: Elaboración propia.
A continuación, se precisa cómo debe suceder el control del PEA del CDI desde la perspectiva del enfoque profesional y en función de evaluar el desarrollo de la creatividad de los estudiantes. Este, se enfoca hacia el control de la solución de los problemas profesionales y de su incidencia en el desarrollo de la creatividad por parte del profesor y guía a los estudiantes hacia la valoración de lo que ellos y sus compañeros realizan al resolver las tareas.
Para su realización se sugiere un quinto procedimiento que se utiliza por profesores y estudiantes durante la solución de las tareas del PEA del CDI. Las acciones que este incluye son las siguientes:
● Obtención y procesamiento de información afín al proceso de solución del problema profesional, a partir del intercambio con estudiantes y entre ellos.
● Intercambio y análisis de los juicios valorativos elaborados con relación al proceso y a los productos derivados de la solución al problema profesional.
● Rediseño, selección y orientación de nuevas tareas relacionadas con la solución del problema profesional y transferencia a otros similares.
Se sugiere, para trabajar con este último procedimiento, que los profesores y estudiantes se enfoquen en conocer y valorar cómo los estudiantes logran resolver los problemas profesionales y, a su vez, desarrollar la creatividad. Para ello, se le recomienda la utilización de métodos variados que le permitan obtener información del proceso de solución de las tareas y de su incidencia en el desarrollo de la creatividad; el diseño de instrumentos según el objetivo específico a evaluar y, tener en cuenta, las dimensiones, los indicadores planteadas al inicio de este apartado; el procesamiento de la información empleando métodos de la estadística descriptiva y, también, técnicas propias de la investigación cualitativa que le permitan sugerir y estimular el uso de otros métodos o estrategias y la elaboración de productos o materiales que evidencien el proceso de solución seguido y su argumentación y la propuesta de nuevas tareas que estimulen el desarrollo de la creatividad.
De forma general, en dichos intercambios, el profesor debe promover la producción de conocimientos y estimular la motivación de los estudiantes a partir de la variabilidad de los contextos en que puede ser aplicado el CDI. Para ello, es recomendable el trabajo cooperativo, la crítica, la colaboración, la discusión y la defensa de ideas propias.
Derivado de lo anterior, se orientan las nuevas tareas relacionadas con la solución del problema profesional analizado u otros similares y que los estudiantes deberán realizar; según los juicios valorativos que resultaron de la información recopilada.
De los resultados del diagnóstico y del análisis de la metodología descrita emerge como limitación del estudio la carencia y poca variedad de estrategias que estimulen el desarrollo de la creatividad de los estudiantes desde el PEA del CDI, viéndose como futura línea de investigación la necesidad de fundamentar teórica y metodológicamente nuevas estrategias creativas; así como la necesidad de contar o elaborar situaciones problemáticas propias de la contabilidad y las finanzas que se solucionen aplicando el CDI.
Por último, la Figura 2 muestra la estructura externa y las relaciones internas de cada una de las partes de la metodología.
Conclusiones
La metodología se sustenta desde el punto de vista teórico en la concepción de un PEA desarrollador, que se distingue por promover la formación integral de los estudiantes a partir de estimular la activación-regulación, la significatividad y la motivación por el aprendizaje del CDI. Asimismo, prioriza el uso de la modelación y de los problemas como estrategias que, centradas en el enfoque profesional del contenido, estimulan el desarrollo de la creatividad.
Figura 2.
Representación gráfica de la metodología
Fuente: Elaboración propia.
Los resultados del diagnóstico permitieron identificar como causas principales que limitan el desarrollo de la creatividad de los estudiantes de la Carrera Contabilidad y Finanzas en el PEA del CDI el limitado vínculo entre estos contenidos y los de la profesión. De igual forma, se constató la existencia de debilidades relacionadas con la motivación por el aprendizaje, los procedimientos de cálculo de derivadas e integrales, así como poca originalidad e independencia durante la realización de tareas relacionadas con estos contenidos.
La metodología, vista como principal aporte del estudio, es contentiva de cuatro procedimientos que orientan la actuación del profesor y de los estudiantes durante la planificación, ejecución y evaluación del PEA del CDI. Se distingue por la utilización del enfoque profesional del contenido para lograr el desarrollo de la creatividad de los estudiantes de la Carrera Contabilidad y Finanzas a partir del cumplimiento de las exigencias que precisa como condicionantes imprescindibles para su instrumentación en la práctica. En ella se usan, de manera combinada, estrategias, medios, procedimientos heurísticos y tareas que favorecen el desarrollo de la creatividad a partir del enfoque profesional.
La pesquisa aportó como futuras líneas de investigación e innovación didáctica: la carencia y poca variedad de estrategias que estimulen el desarrollo de la creatividad de los estudiantes desde el PEA del CDI y de situaciones problemáticas propias de la contabilidad y las finanzas que se solucionen mediante la aplicación del referido contenido.
Referencias
Alonso, L. A., Leyva, P. A. y Mendoza, L. L. (2019). La metodología como resultado científico: alternativa para su diseño en el área de ciencias pedagógicas. Opuntia Brava, 11(2), 231-247. https://opuntiabrava.ult.edu.cu/index.php/opuntiabrava/article/view/915/1032
Álvarez, M., Almeida, B. y Villegas, E. V. (2014). El proceso de enseñanza-aprendizaje de la Matemática. Documentos metodológicos. Editorial Pueblo y Educación.
Armada, L., Arteaga, E. y Del Sol, J. L. (2016). El desarrollo de la creatividad en la enseñanza de la Matemática. El reto de la educación Matemática en el siglo XXI. Revista Conrado, 12(54), 84-92. http://conrado.ucf.edu.cu/index.php/conrado/article/download/371/pdf/658
Ayllón, M., Gómez, I. y Ballesta, J. (2016). Pensamiento matemático y creatividad a través de la invención y resolución de problemas matemáticos. Propósitos y Representaciones, 4(1), 169-218. http://dx.doi.org/10.20511/pyr2016.v4n1.89
Ballester, S., García, J. E., Almeida, B., Álvarez, M., Rodríguez, M., González, R. A. y Puig, N. (2018). Didáctica de la Matemática (Tomo 1). Editorial Pueblo y Educación.
Calero, N. (2005). El modo de actuación creativo del profesor en formación [Tesis de doctorado inédita]. Universidad de Ciencias Pedagógicas “Félix Varela”.
Chávez, C. F. y Rojas, O. J. (2021). Algunas consideraciones sobre el pensamiento divergente y la creatividad a partir de la resolución de un problema geométrico con múltiples vías de solución. Números, 107(marzo), 91-108. https://dialnet.uniroja.es/servlet/articulo?codigo=7830306
Concepción, M. L., Remedios, J. M. y Hernández, T. (2017). Barreras asociadas a la creatividad de los docentes: una propuesta de solución. Revista Pedagogía y Sociedad, 20(49), 48-64. http://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/516
De Bono, E. (2000). El pensamiento lateral. Manual de creatividad. Editorial Paidós.
De La Fuente, E., Robledo, D. E. y Ventura, R. (2019). Desaxiomatización en la enseñanza matemática para fomentar la creatividad. Praxis Investigativa Redie, 11(21), 48-54. https://dialnet.unirioja.es/servlet/articulo?codigo=7145128
De La Torre, S. (2003). Dialogando con la creatividad. De la identificación a la creatividad paradójica. Ediciones Octaedro.
De Prado, D. (2005). La relajación creativa integral. Santiago de Compostela.
Díaz, A. y Mitjáns, A. (2013). Creatividad y subjetividad: su expresión en el contexto escolar. Diversitas: Perspectivas en Psicología, 9(2),427-434. https://www.redalyc.org/pdf/679/67932397014.pdf
Fortes, E. C. y Andrade, R. R. (2019). Mathematical Creativity In Solving Non-Routine Problems [Creatividad matemática en la resolución de problemas no rutinarios]. The Normal Lights, 13(1), 108-135. https://po.pnuresearchportal.org/ejournal/index.php/normallights/article/view/1237
Gibert, E. M. y Ballester, S. (2013). Promoviendo el aprender a aprender matemática en las clases de la Educación Secundaria Básica. Atenas, 1(21), 103-118. https://www.redalyc.org/pdf/4780/478048957007.pdf
Guilford, J. (1980). La creatividad. Editorial Narcea.
Jara, M. A. (2017). Cálculo Integral y sus Aplicaciones en la Empresa. Universidad ECOTEC.
Lao, L., Fuentes, A. y Tamayo, R. M. (2020). El tratamiento al enfoque profesional en el proceso de enseñanza aprendizaje de la Educación Superior. Luz, 19(2), 122-127. https://www.redalyc.org/journal/5891/589164533012/589164533012.pdf
Leyva, P. A. (2013). Las exigencias de los trabajos científicos [Material orientador inédito]. Universidad de Ciencias Pedagógicas de Holguín.
Minaya, D. R. (2017). Guía didáctica para la resolución de problemas de aplicación de la integral definida, en la carrera de economía de la universidad laica Eloy Alfaro de Manabí [Tesis de maestría inédita]. Universidad de Holguín. Oscar Lucero Moya.
Ministerio de Educación Superior de Cuba (2016). Modelo del profesional. Plan de estudio “E” [Manuscrito inédito].
Ministerio de Educación Superior de Cuba (2017). Plan de estudio “E”. Licenciatura en Contabilidad y Finanzas [Manuscrito inédito].
Ministerio de Educación Superior de Cuba (2018). Modelo del profesional. Plan de estudio “E” Licenciatura en Contabilidad y Finanzas [Manuscrito inédito].
Mitjáns, A. (2013). Aprendizaje creativo: desafíos para la práctica pedagógica. Revista CS, (11), 311-341. https://www.redalyc.org/pdf/4763/476348374010.pdf
Moncada, K. L. (2002). Aplicación de la Matemática a la Economía. [Tesis de licenciatura]. Universidad de Los Andes del Tachira. https://www.researchgate.net/profile/Miguel-Vera-2/publication/44354663_Aplicacion_de_la_matematica_a_la_economia_Keila_Loana_Moncada_Araque/links/592cc0cfaca27295a8159d0f
Moreno, M. C. (2019). El aprendizaje creativo en la matemática, su contribución a la formación del ingeniero industrial. Atenas, 2(46), 47-55. https://www.redalyc.org/articulo.oa?id=478060100004
Osborn, A. (1953). Applied imagination. Principles and Procedures of creative. Charles Schibner´s Sons.
Quimis, J. R., Barberán, J. P. y Roca, P. (2019). Creatividad profesional: necesidad de la universidad actual. Opuntia Brava, 11(Especial 1), 35-44. https://opuntiabrava.ult.edu.cu/index.php/opuntiabrava/article/view/656
Ramírez, E. (2016). El cálculo en la formación de competencias profesionales de contadores. Revista Boletín Redipe, 5(8), 61-75. https://revista.redipe.org/index.php/1/article/view/120
Rico, P. y Silvestre, M. (2002). Proceso de enseñanza aprendizaje. Breve referencia al estado actual del problema. En G. García-Batista (Coord.), Compendio de Pedagogía (pp. 68-79). Editorial Pueblo y Educación.
Ríos, P. y Bravo, G. (2017). La creatividad en el proceso de enseñanza-aprendizaje en la educación superior: una necesidad impostergable. Qualitas, 13, 133-150. https://scholar.google.com/scholar?hl=es&as_sdt=0,5&cluster=7067777854833251392
Rodríguez, A. (2018). Estrategia didáctica para la enseñanza-aprendizaje del cálculo diferencial con enfoque profesional en la Facultad Introductoria de Ciencias Informáticas [Tesis de maestría inédita]. Universidad de La Habana. https://repositorio.uci.cu
Rojas, A. y Rodríguez, J. B. (2021). La significatividad del aprendizaje del cálculo diferencial e integral. VARONA, Revista Científico-Metodológica, (72), 11-15. http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1992-82382021000100011
Saborido, R. (2020). Universidad y desarrollo sostenible. Visión desde Cuba [Sesión en Congreso]. Discurso pronunciado en la inauguración del XII Congreso Internacional de Educación Superior “UNIVERSIDAD 2020”. La Habana, Cuba.
Sánchez, W., Pérez, A. y Remedios, J. M. (2022). El aprendizaje creativo: una alternativa para el proceso de enseñanza y aprendizaje de la matemática. Pedagogía y Sociedad, 25(63), 290-309. http://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/1278
Santos, Y. y Armas, C. B. (2018). Algunas exigencias didácticas para el proceso de enseñanza- aprendizaje en las carreras de ciencias técnicas [Presentación en congreso]. 11no. Congreso Internacional de Educación Superior “Universidad 2018”. La Habana, Cuba.
Torrance, P. (1979). La enseñanza creativa. Santillana.
Uribe, N., Ulloa, J. y Flores, J. F. (2020). Razón de cambio basada en el uso de dispositivos móviles. Acta Latinoamericana de Matemática Educativa, 33(20), 95-105. https://funes.uniandes.edu.co/wp-content/uploads/tainacan-items/32454/1179163/Uribe2020Razon.pdf
Valdés, J. M. y Páez, M. (2021). Caracterización del estado actual del proceso de enseñanza-aprendizaje del Cálculo I en la carrera de Ingeniería Informática de la Universidad de Pinar del Río “Hermanos Saíz Montes de Oca”. Mendive, 19(2), 406-417. https://mendive.upr.edu.cu/index.php/MendiveUPR/article/view/2414
Vázquez, C. (2003). Estrategia metodológica para la integración de la Física y la Matemática en décimo grado [Tesis de maestría inédita]. Instituto Superior Pedagógico José Martí.
Villena, M. y Rivas, N. (2019). Impacto del uso de la tecnología en el proceso de enseñanza- aprendizaje del cálculo integral. Revista Conrado, 15(68), 297-307. http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1990-86442019000300297
Viñamagua, G. (2017). Concepción integradora del cálculo diferencial en Cálculo I, carrera de economía de la Universidad Técnica Particular de Loja, Ecuador [Tesis de maestría inédita]. Universidad de Holguín Oscar Lucero Moya.
Yánez, P. (2016). El proceso de aprendizaje: fases y elementos fundamentales. Revista San Gregorio, 1(11), 70-81. https://dialnet.unirioja.es/servlet/articulo?codigo=5585727
Zambrano, N. I. (2019). El desarrollo de la creatividad en estudiantes universitarios. Revista Conrado, 15(67), 355-359. http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1990-86442019000200354