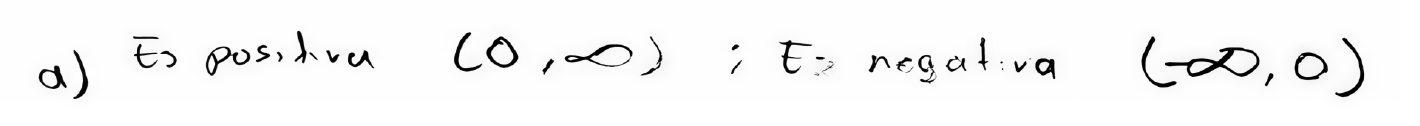resumen

En este artículo se presentan los resultados de la aplicación de un cuestionario diseñado para evaluar las dificultades de aprendizaje que enfrenta el estudiantado de programas de ingeniería al abordar ciertos conceptos específicos de la derivada. El cuestionario fue aplicado a 11 estudiantes de las carreras de ingeniería industrial, civil y automatización. Para el análisis de las respuestas, se utilizaron algunas nociones teóricas y metodológicas proporcionadas por el Enfoque Ontosemiótico (EOS) del Conocimiento y la Instrucción Matemáticos. Los hallazgos indican que el 55% del estudiantado evidenció el significado de la derivada como razón de cambio, y que existe una preferencia por el uso del registro algebraico. Finalmente, se presentan reflexiones sobre las tareas que deberían integrarse en los cursos de cálculo para mejorar la formación del estudiantado en ingeniería.

PALABRAS CLAVE: Derivada, Formación en ingeniería, Cálculo, Comprensión.

ABSTRACT

This article reports on the findings attained from a questionnaire to assess learning difficulties encountered by engineering students regarding concepts about derivatives. The questionnaire was distributed to eleven students enrolled in the industrial, civil, and automation engineering programs. Analysis of the responses utilized theoretical and methodological concepts from the Ontosemiotic Approach (OSA) to Mathematical Knowledge and Instruction. Based on the results, 55% of students demonstrated comprehension of derivatives as a rate of change and preferred the algebraic representation. Final recommendations are provided regarding tasks that should be integrated into calculus courses to strengthen the training of engineering students. This article presents the results of applying a questionnaire designed to evaluate the learning difficulties faced by engineering students when addressing specific concepts of the derivative.

KEYWORDS: Derivatives, Engineering Education, Calculus, Understanding.

INTRODUCción

La enseñanza de las matemáticas en las carreras de ingeniería ha sido objeto de estudio por numerosos investigadores en el campo de la educación matemática durante varias décadas. Esto se debe al papel importante que desempeñan las matemáticas en el desarrollo del pensamiento sistemático, lógico, crítico y el razonamiento abstracto. Estas habilidades permiten a estudiantes de ingeniería interpretar, plantear y resolver problemas específicos de su carrera, así como enfrentar los desafíos del siglo y tomar decisiones informadas en su práctica profesional (Loachamín et al., 2023).

Diversos estudios han analizado cómo se abordan los conceptos matemáticos dentro del contexto de la ingeniería, con el objetivo de mejorar la formación del estudiantado y su capacidad para resolver problemas ingenieriles (Gnedeko & Khalil, 1979; Hieb et al., 2015; Neubert et al., 2014; Randahl, 2016; Sonnert & Sadler, 2014). Estos estudios sugieren que las matemáticas deben presentarse al estudiante de ingeniería como una herramienta de investigación, utilizando ejemplos claros que demuestren su utilidad en la resolución de problemas reales. También destacan que los recursos tecnológicos y los libros de texto son herramientas valiosas, pero su efectividad depende de cómo se usen e integren en el proceso educativo. Además, destacan la necesidad de abordar factores emocionales, como la gestión del tiempo, la orientación de metas y la ansiedad ante los exámenes, los cuales influyen en el rendimiento académico del estudiantado que se forma en ingeniería.

En este contexto, uno de los conceptos matemáticos más estudiados es la derivada, debido a sus diversas aplicaciones en las ciencias y la ingeniería. Se han realizado numerosos estudios sobre la complejidad de sus significados, sus múltiples representaciones (gráficas, numéricas, verbales y simbólicas), los procesos de enseñanza y aprendizaje, incluyendo el uso de la tecnología, la idoneidad epistémica de sus significados en los distintos currículos y el análisis de sus significados parciales en los libros de texto universitarios para las carreras de ingeniería (Galindo et al., 2023; Galindo & Breda, 2023; Kunwar & Laxmi, 2023; Larios et al., 2021; Larios & Jiménez, 2022; Ozaltun-Celik, 2021; Pino-Fan et al., 2016; Rodríguez-Nieto et al., 2022).

El estudiantado de ingeniería enfrenta obstáculos en la comprensión de la derivada, en parte debido a su abstracción y a la complejidad de su significado holístico (Pino-Fan et al., 2016). Estudios han identificado diversas áreas problemáticas: 1) la construcción del significado de una tangente como límite de rectas secantes y su aplicación en contextos económicos; 2) la dificultad en la conversión entre diferentes registros semióticos; 3) obtención de máximos y mínimos centrándose únicamente en un proceso algebraico, lo que obstaculiza la comprensión de optimización de funciones; y 4) una interpretación inadecuada de la derivada como una razón de cambio. En general, las investigadoras y los investigadores coinciden en que estas dificultades se originan en una enseñanza predominantemente algorítmica, o con un enfoque riguroso y formalista que descuida la comprensión de los principios básicos del cálculo y sus aplicaciones prácticas en ingeniería, limitando así su utilidad para resolver problemas específicos en la profesión (Andrade-Aréchiga et al., 2012; Fúneme, 2019; Galindo et al., 2022; Garcés, 2021; Manjarrez-Pontón & Romero-Rincón, 2022; Ruiz-Ledesma, 2019; Torreblanca, 2021; Verón et al., 2022).

Este artículo busca identificar los significados que el estudiantado de ingeniería asigna a la derivada en sus prácticas matemáticas, en relación con ciertas tareas específicas sobre este concepto. Conocer estos significados parciales no solo permite adaptar los currículos a las necesidades reales de las futuras personas profesionales en ingeniería, sino que también ayuda a desarrollar mejores estrategias de enseñanza y aprendizaje que faciliten al estudiantado la comprensión de conceptos más avanzados del cálculo, relevantes en los estudios de ingeniería.

En cuanto a la estructura del presente artículo, esta considera las bases conceptuales del Enfoque Ontosemiótico centradas en el análisis de la actividad matemática, el procedimiento metodológico con un enfoque cualitativo, la descripción del perfil del estudiantado, la presentación de los resultados y la discusión, así como las conclusiones y recomendaciones orientadas a mejorar la enseñanza de algunos significados de la derivada en los programas de ingeniería.

Marco Teórico

El Enfoque Ontosemiótico (EOS) de investigación en didáctica de la matemática es un sistema teórico, integral y flexible que busca ofrecer herramientas metodológicas y principios que aborden y articulen los problemas epistemológicos, cognitivos, afectivos, interaccionales, mediacionales y ecológicos presentes en los procesos de enseñanza y aprendizaje de las matemáticas. Según Lugo-Armenta y Pino-Fan (2021), “el significado de un objeto matemático es entendido en el EOS como el sistema de prácticas operativas y discursivas que una persona o una institución desarrolla para resolver cierto tipo de situaciones/problemas en los que interviene dicho objeto matemático” (p. 1779). Así, se distinguen dos tipos de significados: institucional y personal (Godino, 2022).

Para realizar un análisis detallado y sistemático de las prácticas matemáticas, el EOS introduce una tipología de objetos matemáticos primarios: problemas, elementos lingüísticos, definiciones, proposiciones, procedimientos y argumentos. Estos objetos forman redes llamadas configuraciones, que pueden ser epistémicas (institucionales) o cognitivas (personales). En este trabajo, se utilizó la configuración cognitiva para analizar las prácticas matemáticas del alumnado de ingeniería en relación con las tareas específicas asignadas, las cuales serán descritas en el apartado siguiente.

Por otra parte, en el EOS, la complejidad de un objeto matemático se relaciona con la pluralidad de sus significados, derivados de diversas prácticas matemáticas a lo largo de su evolución en contextos específicos. Por ejemplo, Pino-Fan (2014) realizó un estudio histórico-epistemológico de la derivada, identificando nueve significados parciales, desde la idea de la recta tangente en la geometría griega hasta la definición formal basada en el límite. La caracterización de estos significados proporciona elementos para diseñar cuestionarios que evalúan la comprensión de este concepto tanto en estudiantes como en docentes en formación (Pino-Fan et al., 2015).

Metodología

La investigación es de tipo exploratorio y se enmarca en una metodología cualitativa (Merrian & Tisdell, 2015), con un diseño de estudio de caso. Este enfoque se centra en investigar un fenómeno o situación en su contexto real mediante el estudio de casos particulares. Por esta razón, se utiliza un grupo reducido de participantes, lo que permite un análisis más profundo y detallado del fenómeno en cuestión (Jiménez, 2012; Reyes, 2021).

El estudio de caso, al centrarse en un caso específico o en unos pocos, no permite hacer generalizaciones. Estos estudios no pretenden representar una muestra de una población, sino que se enfocan en el desarrollo de teorías mediante una generalización analítica, en lugar de basarse en generalizaciones estadísticas (Chaves & Comet, 2016; Enrique & Barrio, 2018).

En este contexto, el presente estudio se centró en la observación de variables cualitativas como las configuraciones cognitivas asociadas a las prácticas matemáticas del estudiantado respecto a la derivada, a través del análisis de sus respuestas, describiendo los objetos matemáticos primarios que conforman dichas configuraciones. Además, se emplearon estadísticas descriptivas para analizar variables cuantitativas, como el grado de precisión en las respuestas clasificadas como correctas, parcialmente correctas o incorrectas.

Para la recolección de datos, se aplicó un cuestionario con el objetivo de evaluar la comprensión de la derivada de estudiantes universitarios. Este cuestionario se realizó en una sesión de dos horas. Se explicó a las personas participantes su estructura, indicando que formaba parte de una investigación en curso, y se les aseguró que su identidad sería protegida, siendo identificadas como estudiante E seguido de un número correspondiente, por ejemplo, E1.

El cuestionario

El cuestionario utilizado para evaluar la comprensión del estudiantado sobre la derivada consta de seis tareas, identificadas con la letra “T” seguida de un número, algunas de las cuales incluyen subtareas. Este es el caso de las tareas 1, 4 y 5, que constan de dos incisos cada una, por lo que se denominaron T1a, T1b, T4a, T4b, T5a y T5b, respectivamente. Cada tarea está estrechamente vinculada a los nueve significados parciales de la derivada, los cuales fueron identificados a través de un estudio histórico-epistemológico cuyo objetivo fue reconstruir el significado holístico de este concepto matemático (Pino-Fan et al., 2016). En la Tabla 1 se describen las tareas y se especifican los objetivos que persiguen.

Tabla 1.

Resumen de las características del instrumento

Tarea	Objetivo	Representación que moviliza	Significado parcial asociado
Tarea 1: Identificación de los ceros de la derivada	Establecer conexiones entre distintos significados de la derivada.	Simbólica y gráfica	Tangentes
Tarea 2: Aproximación de la derivada a partir de una tabla de valores	Explorar el significado de la derivada en un punto a partir de la aproximación numérica	Tabular y simbólica	Variación/razón de cambio
Tarea 3: Cálculo de la derivada en un punto a través de un registro gráfico	Relacionar la pendiente de la recta tangente a la gráfica de la función en un punto con el valor de la derivada en dicho punto.	Gráfica y simbólica	Tangentes
Tarea 4: Interpretación de la derivada como razón de cambio	Asociar la derivada como una tasa de cambio instantánea a través de un fenómeno físico.	Simbólica	Variación/razón de cambio
Tarea 5: Análisis de la derivada a partir de la gráfica de la función original	Identificar las variaciones de la función derivada observando el comportamiento de la gráfica de la función original.	Gráfica	Tangentes
Tarea 6: Gráfica de la derivada de una función definida a trozos	Identificar características importantes de la derivada de una función a trozos mediante su representación gráfica	Gráfica	Tangentes/límites

Fuente: Elaboración propia a partir de Larios et al. (2021).

Participantes y contexto

El cuestionario se aplicó a 11 estudiantes de los programas de Ingeniería Civil, Automatización e Industrial, quienes cursaban el segundo semestre y estaban inscritos en la asignatura de Cálculo Multivariable. Los y las participantes cumplían con los prerrequisitos de la materia, que consisten en la aprobación de los cursos de Cálculo Diferencial, Cálculo Integral y Álgebra Lineal. El rango de edad del estudiantado era de 18 a 22 años.

Es importante señalar que quien realizó la investigación se limitó únicamente a aplicar el cuestionario, explicando a las personas participantes su estructura sin proporcionar información sobre las respuestas. Además, no hubo interacción entre el alumnado y la persona docente a cargo durante el proceso de aplicación.

Resultados y discusión

En esta sección se presenta el análisis de las subtareas T1a, T4b y T5b. No se incluyó el análisis del resto de las tareas debido a que no se obtuvo información relevante, ya que la mayoría de las respuestas fueron incorrectas o los estudiantes se abstuvieron de responder, lo cual refleja un alto grado de dificultad en esas tareas. Estas dificultades coinciden con lo señalado por Sánchez- Matamoros et al. (2008) quien menciona que, aunque los y las estudiantes aplican correctamente las reglas de derivación, presentan dificultades para comprender el significado de la derivada, tanto como límite del cociente incremental como en su interpretación geométrica, relacionada con la pendiente de la recta tangente.

Este problema se debe a que la enseñanza del cálculo se centra únicamente en lo algebraico, sin incluir otras formas de representación, ya que al estudiantado le resulta difícil comprender los conceptos si no desarrolla habilidades visuales que le ayude en la construcción de dichos conceptos. Esto puede hacer que perciban el cálculo solo como un conjunto de fórmulas, perdiendo de vista su propósito principal (García, 2013; Hitt, 2003).

En el análisis de los datos cuantitativos obtenidos con el instrumento, se consideró la variable de grado de corrección de las tareas: correctas (C), parcialmente correctas (PC), incorrectas (I) y sin respuesta (SR). Se realizó un conteo de las respuestas del estudiantado, calculando las frecuencias y los porcentajes correspondientes a cada categoría de corrección.

En cuanto a la variable cualitativa, se utilizó la noción de configuración cognitiva para identificar los objetos matemáticos (elementos lingüísticos, conceptos/definiciones, proposiciones/propiedades, procedimientos y argumentos) involucrados en la resolución de cada tarea, lo que permitió categorizar las respuestas según los tipos de prácticas matemáticas empleadas.

Tarea 1: Identificación de los ceros de la función derivada

La Tarea 1 (Ver Figura 1), fue adaptada del trabajo de Gutiérrez (2006). Los ítems a) y b) de forma independiente evalúan los conocimientos que tiene el estudiantado respecto a la derivada como pendiente de la recta tangente y razón instantánea de cambio. Sin embargo, el objetivo central de la tarea consiste en que las personas participantes mediante su práctica matemática establezcan asociaciones entre estos dos significados de la derivada.

Figura 1.

Tarea 1 del cuestionario.

Fuente: Elaboración propia.

En la Tabla 2 se presentan las frecuencias de cada tipo de configuración, así como el porcentaje del grado de corrección de la tarea. Se puede observar que la configuración cognitiva más utilizada por el estudiantado (27.2%), fue la de obtención del valor extremo y que la mayoría de las respuestas se consideraron incorrectas (45.5%) y parcialmente correctas (27.3%).

Tabla 2.

Tipo de configuración y grado de corrección de T1a

Tipo de configuración cognitiva		Frecuencia	%	Porcentaje por tipo de respuesta
				C	CP	I
Obtención del valor extremo		3	27,2%		18%
Determinación del número crítico		2	18.2%		9.1%
Asociada a la gráfica de l(x)		2	18.2%			9.1%
Cálculo de la derivada		1	9.1%			9.1%
Punto de corte con los ejes		1	9.1%			9.1%
Uso de un registro tabular		1	9.1%			9.1%
Propiedades de una función		1	9.1%			9.1%
Total		11	100%	27.2%	27.3%	45.5%

Nota. La tabla muestra las configuraciones cognitivas y el número de respuestas correctas (C), parcialmente correctas (PC) e incorrectas (I) para cada configuración.

Fuente: Elaboración propia

Un ejemplo de configuración más usada se muestra en la Figura 2. Se observa que, aunque el estudiante o la estudiante encontró correctamente el punto en donde la recta tangente es horizontal, su explicación se centró únicamente en el cálculo algebraico. Se esperaba que explicara que igualar la derivada a cero es esencial porque en esos puntos, la pendiente de la recta tangente a la curva es nula, lo que implica que dicha recta es horizontal. Esta dificultad refleja lo señalado por Ruiz-Ledesma (2019), quien observó que el estudiantado suele enfocarse en seguir pasos memorizados en lugar de aplicar un razonamiento profundo en el proceso de determinación de valores extremos de la función.

Figura 2.

Respuesta del estudiante E7 a T1a.

Fuente: Elaboración propia.

En la Figura 3 se muestra el ejemplo de una respuesta parcialmente correcta proporcionada por una persona participante, quien derivó la función, la igualó a cero y obtuvo el valor crítico x = 3. Además, señaló que la recta tangente es horizontal en los puntos donde su pendiente es igual a cero. Sin embargo, no determinó el punto específico en el que dicha condición se cumple. Este resultado concuerda con lo encontrando por Galindo et al. (2023), quienes observaron que un grupo de estudiantes de ingeniería comercial presentó dificultad con la interpretación de la función derivada y su representación geométrica.

Figura 3.

Respuesta del estudiante E6 a T1a.

Fuente: Elaboración propia.

La Figura 4 presenta un ejemplo de una respuesta incorrecta en la que una persona estudiante, en lugar de identificar el punto donde la recta tangente a la gráfica de la función es horizontal, determinó el punto de intersección con el eje y de la función. Como explican Galindo y Breda (2023), esta situación refleja que el estudiantado no logra establecer “la relación entre la recta tangente a una curva y la interpretación geométrica de la derivada” (p. 316). Según Hitt (2003), las dificultades que enfrenta el estudiantado en la comprensión de los conceptos de cálculo se deben a que en algunos casos los procesos de enseñanza no promueven la visualización matemática integrada con las diferentes representaciones de un concepto (algebraico, gráfico, verbal).

Figura 4.

Respuesta del estudiante E2 a T1a.

Fuente: Elaboración propia.

Tarea 4: Interpretación de la derivada como razón de cambio

Por su parte, la tarea 4 (Ver Figura 5), se tomó del libro de cálculo diferencial de Zill y Wright (2011). Tanto el inciso a) como el b) tienen como propósito movilizar el significado de la derivada como variación de velocidad. El primero evalúa los conocimientos del estudiantado sobre la velocidad promedio, mientras que el segundo indaga sobre su comprensión de la derivada como razón de cambio instantánea (velocidad instantánea).

Figura 5.

Tarea 4 del cuestionario.

Fuente: Elaboración propia.

Como se mencionó anteriormente, solo se consideraron las respuestas de la segunda parte de esta tarea. En la Tabla 3 se muestra que la configuración de cálculo de la velocidad instantánea (91%) fue la más utilizada por el estudiantado. También se evidencia que más de la mitad de las personas (55%) proporcionaron respuestas correctas, y que el 27% de las respuestas fueron parcialmente correctas. Esto refleja que esta tarea no representó un grado de dificultad para los y las participantes.

Tabla 3.

Tipo de configuración y grado de corrección de T1a

Tipo de configuración cognitiva		Frecuencia	%	Porcentaje por tipo de respuesta
				C	CP	I
Cálculo de la velocidad instantánea		10	91%	55%	27%	9%
Referencia a la función original		1	9%			9%
Total		11		55%	27%	18%

Nota. La tabla muestra las configuraciones cognitivas y el número de respuestas correctas (C), parcialmente correctas (PC) e incorrectas (I) para cada configuración.

Fuente: Elaboración propia

La Figura 6 muestra un ejemplo de una respuesta correcta, en la que se deriva la función posición y luego sustituye el valor de t = 3s para obtener la velocidad instantánea. Además, argumenta la razón del porque la velocidad hallada es negativa. Según Bingolbali et al. (2007), el estudiantado de ingeniería muestra una preferencia por la aplicación de conceptos matemáticos en la resolución de problemas propios de su formación, siendo la noción de derivada como tasa de cambio una de las más empleadas.

Figura 6.

Respuesta del estudiante E8 a T4b.

Fuente: Elaboración propia.

Tarea 5: Análisis de la derivada a partir de la gráfica de la función original

Esta tarea (Ver Figura 7) fue adaptada del trabajo realizado por Habre y Abboud (2006) consistió en que el estudiantado evidenciara los significados parciales de variaciones y máximos y mínimos y lo asociaran con la derivada de la función.

Figura 7.

Tarea 5 del cuestionario.

Fuente: Elaboración propia.

Se esperaba que el alumnado al responder el inciso a), analizara el comportamiento de la función a través de su representación gráfica y reconociera que en la parte izquierda de la curva la función decrece, lo cual indica que su derivada toma valores negativos. En cambio, en la parte derecha de la curva, la función crece, lo que sugiere que la derivada toma valores positivos. En la Tabla 4 se observa que la configuración asociada al registro gráfico (72%) fue la más utilizada por el grupo de estudiantes y que el gran porcentaje de respuestas son correctas (45%).

Tabla 4.

Tipo de configuración y grado de corrección de T5a

Tipo de configuración cognitiva		Frecuencia	%	Porcentaje por tipo de respuesta
				C	CP	I
Cálculo de la velocidad instantánea		8	78%	45%		27%
Referencia a la función original		3	28%		19%	9%
Total		11	100%	45%	19%	36%

Nota. La tabla muestra las configuraciones cognitivas y el número de respuestas correctas (C), parcialmente correctas (PC) e incorrectas (I) para cada configuración.

Fuente: Elaboración propia

Del grupo de estudiantes que utilizó la representación gráfica para su respuesta, el 45% representó correctamente los dos intervalos en los que la función derivada toma valores positivos y negativos, respectivamente. Este resultado se aprecia claramente en la Figura 8.

Figura 8.

Respuesta del E8 a la T5a.

Fuente: Elaboración propia.

El 28% restante del estudiantado que utilizó el registro gráfico para abordar la tarea presentó respuestas incorrectas. En la Figura 9 se muestra el ejemplo de un estudiante que respondió con base al comportamiento de la función original y no el de su derivada.

Figura 9.

Respuesta del E8 a la T5a.

Fuente: Elaboración propia.

Conclusiones

Aunque en la mayoría de los currículos se enfatiza principalmente en el significado parcial de la derivada como el límite del cociente de incrementos (Pino-fan et al., 2013). En este estudio, se observó que el significado parcial predominante fue el de la derivada como razón de cambio. En la tarea T4b se pudo apreciar que el porcentaje de respuestas correctas fue mayor. Sin embargo, en lugar de interpretar la velocidad como la derivada de la función posición, sus argumentos se centraron en la descripción del procedimiento utilizado para dar su respuesta. Esto refleja que no hay una comprensión profunda del concepto.

En la T5a predominó el significado parcial vinculado con los procesos de variación de máximo y mínimo. La mayoría del estudiantado proporcionó su respuesta con base en la gráfica de la función, lo cual reflejó una preferencia por el uso del registro gráfico para resolver la tarea.

El significado menos evidente fue el de la derivada como pendiente de la recta tangente. En la T1a, tres estudiantes utilizaron el significado vinculado a los máximos y mínimos para responder. En este caso, graficaron la función propuesta e indicaron que en el punto más alto (valor extremo) de la función, la recta tangente a la curva es horizontal, en lugar de reconocer que, en ese mismo punto, la pendiente de la recta tangente es nula.

De esta forma, se observó que las personas participantes hicieron la conversión del registro algebraico al gráfico, al representar gráficamente la función original y ubicar el punto más alto. Asimismo, hicieron tratamientos dentro del mismo registro algebraico al derivar la función e igualarla a cero para calcular el punto en dónde la pendiente de la recta tangente a la función es horizontal.

Es importante que el profesorado considere la posibilidad de seleccionar tareas apropiadas en los cursos para ingeniería, que aborden una variedad representativa de los significados parciales de la derivada, con el objetivo de construir un significado global del concepto. Los resultados obtenidos en este estudio, aunque limitados a un grupo de 11 estudiantes, proporcionan indicios relevantes sobre las dificultades conceptuales y preferencias en el uso de registros de representación. Estas observaciones pueden servir como punto de partida para diseñar actividades que promuevan una comprensión más profunda del concepto de derivada. Además, es esencial que el personal docente reconozca que la complejidad de un objeto matemático está vinculada a la pluralidad de significados y que incorpore esta perspectiva en sus procesos de instrucción para fomentar un aprendizaje significativo en el alumnado.

Este tipo de estudios también podría extenderse a otros campos científicos como la biología, la física y la química, donde el concepto de derivada resulta fundamental para comprender y modelar distintos fenómenos.

Referencias

Andrade-Aréchiga, M., López, G., & López-Morteo, G. (2012). Assessing effectiveness of learning units under the teaching unit model in an undergraduate mathematics course [Evaluación de la efectividad de las unidades de aprendizaje bajo el modelo de unidades de enseñanza en un curso de matemáticas de pregrado]. Computers and Education, 59(2), 594-606. https://doi.org/10.1016/j.compedu.2012.03.010

Bingolbali, E., Monaghan, J., & Roper, T. (2007). Engineering students’ conceptions of the derivative and some implications for their mathematical education [Engineering students’ conceptions of the derivative and some implications for their mathematical education]. International Journal of Mathematical Education in Science and Technology, 38(6), 763-777. https://doi.org/10.1080/00207390701453579

Chaves, V. E., & Comet, C. (2016). Los estudios de casos como enfoque metodológico. ACADEMO. Revista de Investigación en Ciencias Sociales y Humanidades, 3(2). https://revistacientifica.uamericana.edu.py/index.php/academo/article/view/54

Enrique, A., & Barrio, E. (2018). Guía para implementar el método de estudio de caso en proyectos de investigación. https://ddd.uab.cat/pub/caplli/2018/196118/proinvare_a2018p159.pdf

Fúneme, C. (2019). El aula invertida y la construcción de conocimiento en matemáticas. El caso de las aplicaciones de la derivada. Teché, Episteme y Didaxis: TED, 45, 159-174. https://doi.org/10.17227/ted.num45-9840

Galindo, M., & Breda, A. (2023). Significados de la derivada en los libros de texto de las carreras de Ingeniería Comercial en Chile Significados. Bolema - Mathematics Education Bulletin, 37(75), 271-295. https://doi.org/10.1590/1980-4415v37n75a13

Galindo, M., Breda, A., & Alvarado, H. (2023). Diseño de un proceso de enseñanza de la derivada para estudiantes de ingeniería comercial en chile. Revista Paradigma, 44(4), 321-350. https://revistaparadigma.com.br/index.php/paradigma/article/view/1386

Galindo, M., Breda, A., Chamorro, D., & Alvarado, H. (2022). Analysis of a teaching learning process of the derivative with the use of ICT oriented to engineering students in Chile [Análisis de un proceso de enseñanza aprendizaje de la derivada con el uso de las TIC orientado a estudiantes de ingeniería en Chile]. Eurasia Journal of Mathematics, Science and Technology Education, 18(7), 1-14. https://doi.org/10.29333/ejmste/12162

Garcés, W. (2021). Análisis de las Pautas que Rigen la Práctica del Profesor en la Enseñanza de Derivadas en Ciencias Básicas en Carreras de Ingeniería. Journal of Research in Mathematics Education, 10(3), 239-268. https://doi.org/10.17583/redimat.7957

García, J. (2013). La problemática de la enseñanza y el aprendizaje del cálculo para ingeniería. Revista Educación, 37(1), 29-42. https://doi.org/10.15517/revedu.v37i1.10627

Gnedeko, B. V., & Khalil, Z. (1979). The mathematical education of engineers [La educación matemática de los ingenieros]. Educational Studies in Mathematics, 10(1), 71-83. https://doi.org/10.1007/BF00311176

Godino, J. D. (2022). Emergencia, estado actual y perspectivas del Enfoque Ontosemiótico en educación matemática. Revista Venezolana de Investigación En Educación Matemática, 2(2), 1-24. https://doi.org/10.54541/reviem.v2i2.25

Gutiérrez, A. (2006). An investigation of students’ understanding and representation of derivative in a graphic calculator-mediated teaching and learning environment [Tesis doctoral, University of Auckland]. https://hdl.handle.net/2292/2161

Habre, S., & Abboud, M. (2006). Students’ conceptual understanding of a function and its derivative in an experimental calculus course [Comprensión conceptual de los estudiantes sobre una función y su derivada en un curso de cálculo experimental]. Journal of Mathematical Behavior, 25(1), 57-72. https://doi.org/10.1016/j.jmathb.2005.11.004

Hieb, J. L., Lyle, K. B., Ralston, P. A. S., & Chariker, J. (2015). Predicting performance in a first engineering calculus course: implications for interventions [Predicción del rendimiento en un primer curso de cálculo de ingeniería: implicaciones para las intervenciones]. International Journal of Mathematical Education in Science and Technology, 46(1), 40-55. https://doi.org/10.1080/0020739X.2014.936976

Hitt, F. (2003). Dificultades en el aprendizaje del cálculo. Undécimo Encuentro de Profesores de Matemáticas del Nivel Medio Superior, 81-107. https://www.academia.edu/807014/Dificultades_en_el_aprendizaje_del_c%C3%A1lculo

Jiménez, V. (2012). El estudio de caso y su implementación en la investigación. Revista Internacional de Investigación En Ciencias Sociales, 8(1), 141-150. https://doi.org/10.1057/9781137430168_3

Kunwar, R., & Laxmi, G. (2023). An Overview of Strategies for Conceptualizing Derivative and their Applications in Daily Life for Secondary-Level Mathematics Students [Una descripción general de las estrategias para conceptualizar la derivada y sus aplicaciones en la vida diaria para estudiantes de matemáticas de nivel secundario]. South Asian Research Journal of Engineering and Technology, 5(5), 69-82. https://doi.org/10.36346/sarjet.2023.v05i05.003

Larios, V., & Jiménez, A. (2022). Significados parciales de la derivada en libros universitarios en la formación de ingenieros. Praxis & Saber, 13(33), e12274. https://doi.org/10.19053/22160159.v13.n33.2022.12274

Larios, V., Páez, R. E., & Moreno, H. (2021). Significados sobre la derivada evidenciados por alumnos de carreras de Ingeniería en una universidad mexicana. Avances de Investigación en Educación Matemática, 20, 105–124. https://doi.org/10.35763/aiem20.4002

Loachamín, H. D., Vargas, Á. P., Andrade, J. V., & Puente, P. F. (2023). Enseñanza, aprendizaje y enfoque de la matemática en la ingeniería. AlfaPublicaciones, 5(3.2), 6–20. https://doi.org/10.33262/ap.v5i3.2.400

Lugo-Armenta, J. G., & Pino-Fan, L. R. (2021). Niveles de Razonamiento Inferencial para el Estadístico t-Student. Bolema - Mathematics Education Bulletin, 35(71), 1776–1802. https://doi.org/10.1590/1980-4415V35N71A25

Manjarrez-Pontón, C. A., & Romero-Rincón, Y. J. (2022). Análisis de las estrategias instruccionales utilizadas para el aprendizaje significativo de la definición de derivada de funciones de una variable. ReHuSo: Revista de Ciencias Humanísticas y Sociales, 7(3), 112–125. https://doi.org/10.33936/rehuso.v7i3.5157

Merrian, S. B., & Tisdell, E. J. (2015). Qualitative Research: A Guide to Design and Implementation [Investigación cualitativa: guía para su diseño e implementación] (4th ed.). Wiley.

Neubert, J., Khavanin, M., Worley, D., & Kaabouch, N. (2014). Minimizing the Institutional Change Required to Augment Calculus With Real-World Engineering Problems [Minimizar el cambio institucional necesario para ampliar el cálculo con problemas de ingeniería del mundo real]. Primus, 24(4), 319–334. https://doi.org/10.1080/10511970.2013.879970

Ozaltun-Celik, A. (2021). A calculus student’s understanding of graphical approach to the derivative through quantitative reasoning [La comprensión por parte de un estudiante de cálculo del enfoque gráfico de la derivada a través del razonamiento cuantitativo]. Lumat, 9(1), 892–916. https://doi.org/10.31129/LUMAT.9.1.1663

Pino-Fan, L. R. (2014). Evaluación de la faceta epistémica de futuros profesores de Bachillerato sobre la derivada [Tesis Doctoral] Universidad de Granada. https://digibug.ugr.es/handle/10481/29940

Pino-fan, L. R., Castro, W., Godino, J. D., & Font, V. (2013). Idoneidad epistémica del significado de la derivada en el currículo de bachillerato. Journal of the American Chemical Society, 34(2), 123–150. https://revistaparadigma.com.br/index.php/paradigma/article/view/522/519

Pino-Fan, L. R., Godino, J. D., & Font, V. (2015). A proposal for the analysis of prospective teachers’ mathematical practices on derivatives [Una propuesta para el análisis de las prácticas matemáticas de futuros profesores sobre derivadas]. Bolema - Mathematics Education Bulletin, 29(51), 60–89. https://doi.org/10.1590/1980-4415v29n51a04

Pino-Fan, L. R., Godino, J. D., & Font, V. (2016). Assessing key epistemic features of didactic-mathematical knowledge of prospective teachers: the case of the derivative [Evaluación de características epistémicas clave del conocimiento didáctico-matemático de futuros profesores: el caso de la derivada]. Journal of Mathematics Teacher Education, 21(1), 63-94. https://doi.org/10.1007/s10857-016-9349-8

Randahl, M. (2016). Engineering students approaching the mathematics textbook as a potential learning tool – opportunities and constraints [Los estudiantes de ingeniería se acercan al libro de texto de matemáticas como una posible herramienta de aprendizaje: oportunidades y limitaciones] [Tesis doctoral, University of Agder]. Agder University Research Archive (AURA). http://hdl.handle.net/11250/2378867

Reyes, S. M. (2021). La tutoría del Programa Todos a Aprender en la formación continua de docentes: estudio de caso. Revista Educación, 45(2), 1-19. https://doi.org/10.15517/revedu.v45i1.42592

Rodríguez-Nieto, C., Rodríguez-Vásquez, M., & Font, V. (2022). Nueva mirada para analizar las conexiones desde dos lentes teóricos: La teoría ampliada de las conexiones matemáticas y el enfoque ontosemiótico. En J. G. Lugo-Armenta, L. R. Pino-Fan, M. Pochulu y W. F. Castro (Eds.), Enfoque Onto-Semiótico del Conocimiento y la Instrucción Matemáticos: investigaciones y desarrollos en América Latina (pp. 193–219). Universidad de los Lagos.

Ruiz-Ledesma, E. F. (2019). Estudio sobre las dificultades que tienen estudiantes de nivel superior en la resolución de problemas de cálculo, y empleo de un Escenario de aprendizaje tecnopedagógico como apoyo en el trabajo del aula. Nova Scientia, 11(23), 258–295. https://novascientia.lasallebajio.edu.mx/ojs/index.php/Nova/article/view/1840/786

Sánchez- Matamoros, G., García, M., & Llinares, S. (2008). La comprensión de la derivada como objeto de investigación en didáctica de la matemática. Revista Latinoamericana de Investigacion en Matematica Educativa, 11(2), 267–296. https://www.relime.org/index.php/relime/article/view/354

Sonnert, G., & Sadler, P. M. (2014). The impact of taking a college pre-calculus course on students’ college calculus performance [El impacto de tomar un curso de pre-cálculo universitario en el desempeño de los estudiantes en cálculo universitario]. International Journal of Mathematical Education in Science and Technology, 45(8), 1188–1207. https://doi.org/10.1080/0020739X.2014.920532

Torreblanca, F. L. (2021). Ingeniería y situación didáctica para el aprendizaje de la derivada en estudiantes de ingeniería de la Universidad Nacional del Altiplano. Revista de Investigaciones, 10(2), 160–172. https://doi.org//10.26788/riepg.v10i2.2644

Verón, M. A., Giacomone, B., & Del Carmen-Benítez, M. (2022). Significados que los estudiantes de ingeniería otorgan al concepto de diferencial. Advances in Engineering and Innovation, 7(15), 2022. https://www.progreso.tecnm.mx/revistaAEI/index.php/aei/article/view/111/190

Zill, D. G., & Wright, W. S. (2011). Matemáticas 1 Cálculo diferencial. Mc Graw Hill.