Abstract
This paper evaluates two methods in order to estimate the poverty at small areas, both were used to correct the direct estimators from the periodical data sources with the help of the only available parametrical data source (Census). The first method is so-called regression-method, of the type Pit = β0 + β1Pio , where Pit are the poverty values at the periodic source data and Pi0 are the corresponding parametric values (Census); and the second one is called shrinking-method, based on an approach of the James-Stein shrinking estimators:
with variance 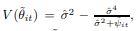
References
Instituto Nacional de Estadística y Censos (2005) Encuesta de Hogares de Propósitos Múltiples de Costa Rica, 2000–2004. San José, Costa Rica. Disponible también en URL: http://encuestas.ccp.ucr.ac.cr.
Farrell, P.J.; MacGibbon, B.; Tomberlin, T.J. (1997) “Empirical Bayes estimators of small area proportions in multistage designs”, Statist. Sinica 7: 1065–1083.
Feres, J.C.; Mancero, X. (2001a) “Enfoques para la medición de la pobreza. Breve revisión de la literatura”, Serie Estudios Estadísticos y Prospectivos 4, CEPAL, Santiago de Chile.
Feres, J. C.; Mancero, X. (2001b) “El método de las necesidades básicas insatisfechas (NBI) y sus aplicaciones en América Latina”, Serie Estudios Estadísticos y Prospectivos 7, CEPAL, Santiago de Chile.
Ghosh, M.; Rao, J.N.K. (1994) “Small area estimation: an appraisal”, Statist. Sci. 9: 55–93.
James, W.; Stein, C.M. (1961) “Estimation with quadratic Llss”, in Proc. 4th Berkeley Symp. Math. Statist. Prob., Vol. 1: 311–319.
Larsen, M.D. (2003) “Estimation of small-area proportions using covariates and survey data”, Journal of Statistical Planning and Inference 112: 89–98.
Malec, D.; Sedransk, J.; Moriarity, C.L.; Leclerc, F.B. (1997) “Small area inference for binary variables in the National Health Interview Survey”, J. Amer. Statist. Assoc. 92: 815–826.
Malec, D.; Davis, W.W.; Cao, X. (1999) “Model-based small area estimation of overweight prevalence using sample selection adjustment”, Statist. Med. 18: 3189–3200.
Manton, J.H.; Krishnamurthy, V.; Vincent Poor, H. (1998) “James-Stein state filtering algorithms”, IEEE Transactions on Signal Processing 46(9).
Programa Estado de la Nación (2005) Undécimo Informe del Estado de la Nación en Desarrollo Humano Sostenible. San José, Costa Rica.
Rao, J.N.K. (2003) Small Area Estimation. Wiley, New York.