Abstract
In this note we evaluate the unidimensional distributional Hankel transform of
and 
and then we extend the formulae to certain kinds of n-dimensional distributions called “causal” and “anti-causal” distributions. We evaluate the distributional Hankel transform of 
, 
and 
.
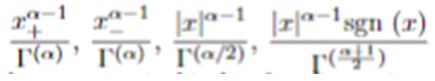
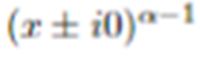
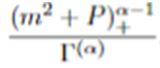
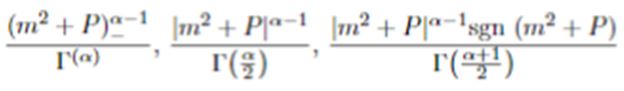
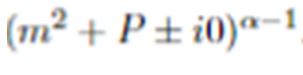
References
Schwartz, L. (1966) Théorie des distributions. Hermann, Paris.
Leray, J. (1952) Hyperbolic Differential Equations. Mimeographed Lecture Notes, Inst. for Advanced Studies, Princeton.
Gelfand, I.M.; Shilov, G.E. (1964) Generalized Functions. Vol I, Academic Press, New York.
Bresters, D.W. (1968) “On distributions connected with quadratic forms”, SIAM J. Appl. Math. 16: 563–581.
Aguirre, M.A.; Trione, S.E. “The distributional Hankel transform of δ(k)(m2+P)”, Studies in Applied Mathematics 83: 111–121, Massachusetts Institute of Technology Publ., Elsevier Science Publ. Co. Inc.
Trione, S.E. (1980) Distributional Products. Cursos de Matemática, N° 3, Serie II, IAM-CONICET.
Trione, S.E. (1987) “The multiplicative product between Pf(m2+P) and δ(γ−1)(m2+P), and others”, Trab. de Matemática, Serie I, N° 130, IAM-CONICET.
Bateman Manuscript (1953) Higher Trascendental Functions, Vol. I and II. McGraw-Hill, New York.
Grandshtegn, I.S.; Ryzhik, I.M. Table of Integrals Series and Products. Corrected and enlarged edition. Academic Press Inc.
Comments
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Copyright (c) 1997 Manuel A. Aguirre